“Il rapporto tra me è la mia ombra è uguale a quello tra la piramide e la sua. Se ne può dedurre che, nell’attimo in cui la mia ombra sarà uguale alla mia statura, l’ombra della piramide sarà uguale alla sua altezza!” Eccola, l’idea tanto cercata. Tuttavia doveva ancora metterla in atto. Talete non poteva compiere quell’operazione da solo: occorreva essere in due. Il fellah accettò di aiutarlo.
Forse tutto questo non è avvenuto realmente. Ma come si fa a saperlo?
L’indomani all’alba, il fellah si diresse verso il monumento, sedendosi all’ombra immensa della piramide. Talete tracciò sulla sabbia un cerchio col raggio uguale alla sua altezza, si pose al centro e si tenne ben dritto, poi concentrò lo sguardo sull’estremità della sua ombra.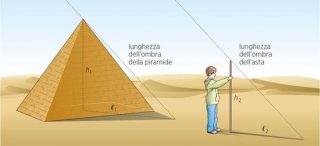 
Quando questa sfiorò la circonferenza, vale a dire quando la lunghezza dell’ombra fu uguale alla sua statura, lanciò il grido stabilito come segnale. Il fellah, che stava appostato, piantò subito un piolo nel punto in cui arrivava l’estremità dell’ombra della piramide, e Talete corse verso il piolo.
Insieme, senza scambiarsi una parola, con l’aiuto della corda ben tesa, misurarono la distanza che separava il piolo dalla base della piramide. Quando ebbero calcolato la lunghezza dell’ombra, ebbero l’altezza della piramide. […]
La verticale mi è inaccessibile? All’ora la raggiungerò grazie all’orizzontale. Non posso misurare l’altezza perché si perde nel cielo? Allora misurerò la sua ombra schiacciata al suolo.
